衍射的原理和类别
原理:子波相干叠加
从同一波面上各点发出的子波都是相干的,在各子波传播到的空间某一点上,该点的光强是所有到达该点的子波相干叠加的结果。
(积分式无需掌握)
类别:菲涅尔衍射、夫琅禾费衍射
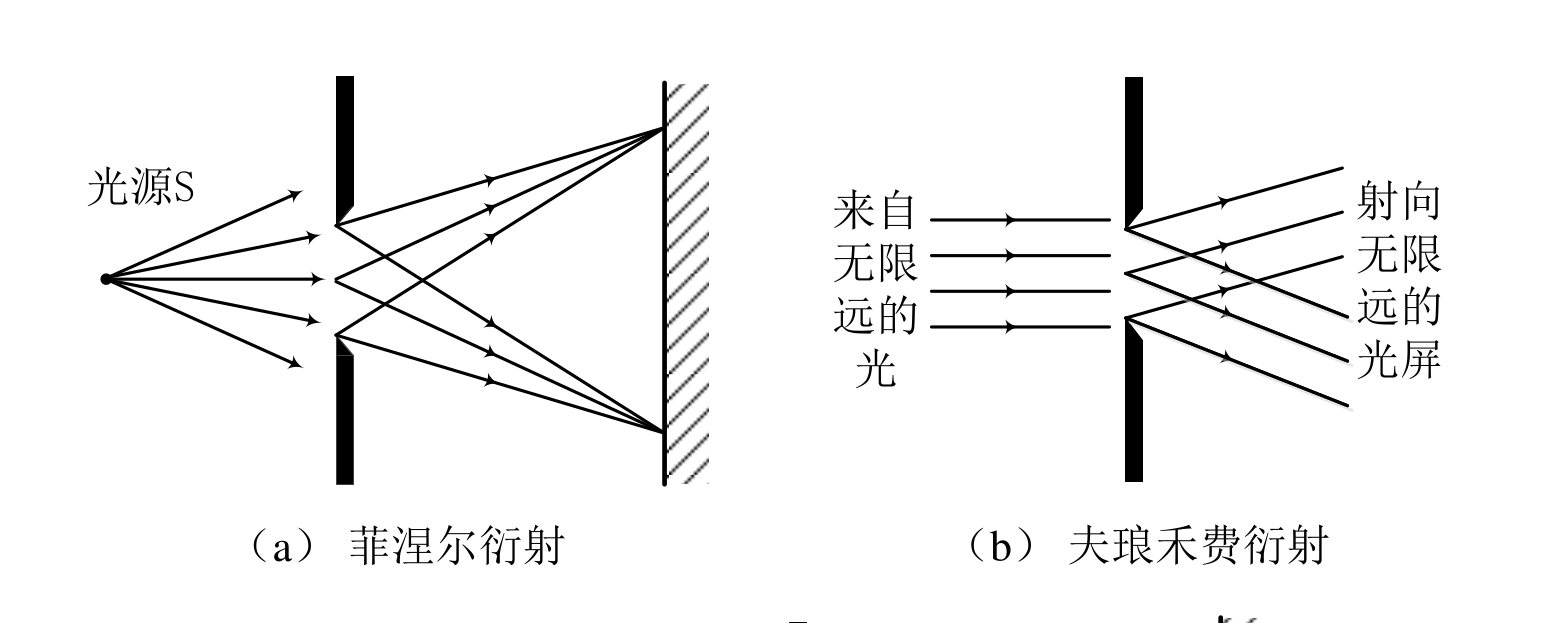
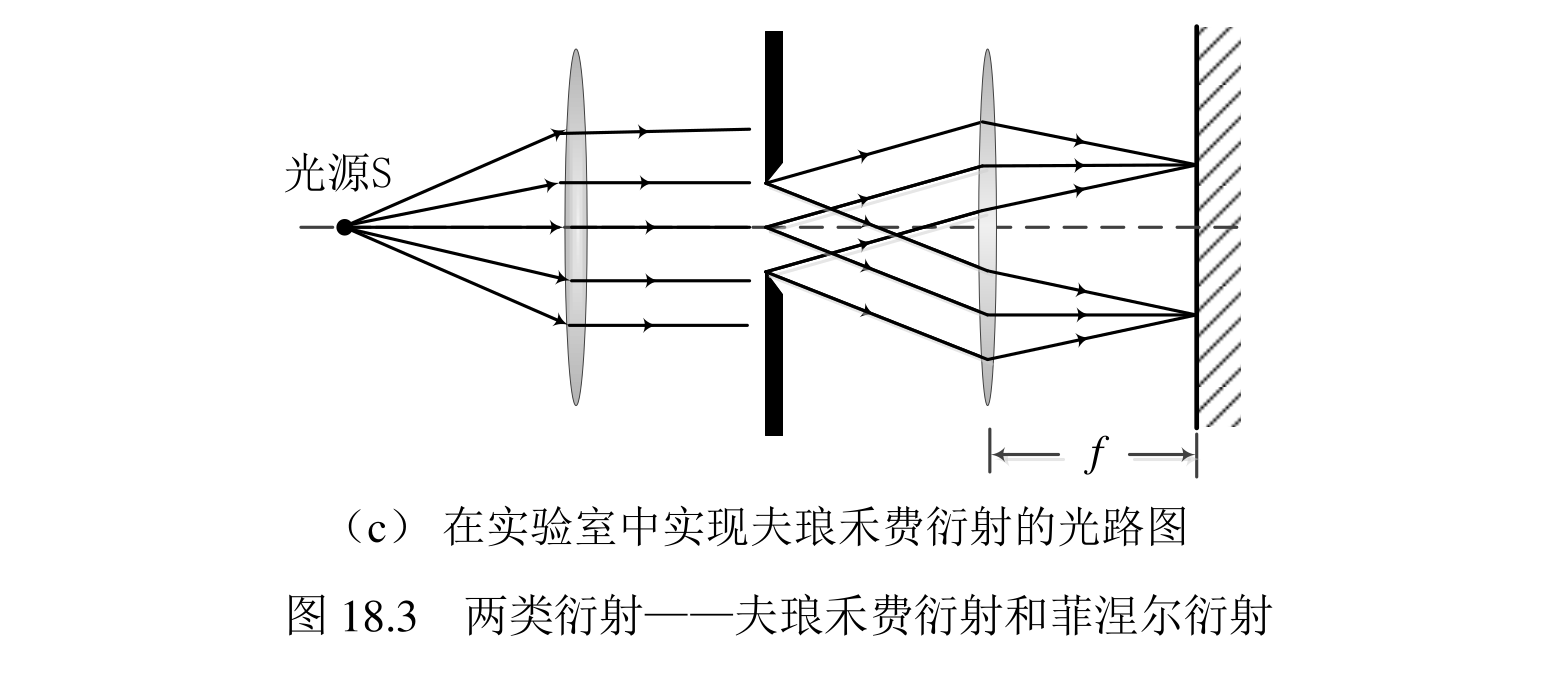
单缝的夫琅禾费衍射
接下来分析夫琅禾费衍射
半波带法分析
凸透镜不引起附加光程差
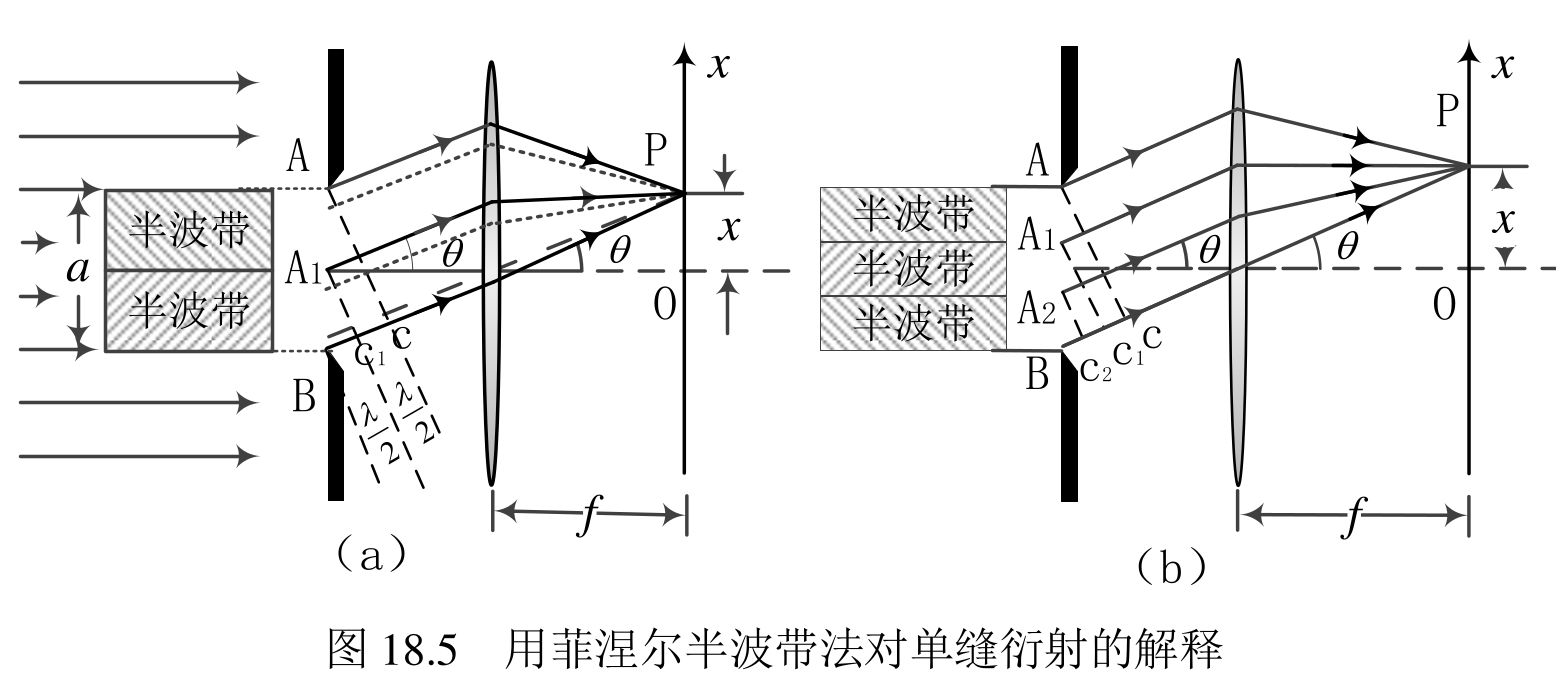
相当于依据角度制定了一个“比例尺”,将原来的光波带划分成了多个半波带。
如此可以解释两个现象:
部分位置没有光:相邻半波带会被两两抵消。
越远光强越弱:因为最终有效半波带最多只有1个,而越远划分越细,因此也会导致光强越弱。
抵消的关系可以参考“三角形全等”,不过这个是我的理解()
最终我们可以提炼出一个(或者两个)精简的公式:
暗纹条件:
asin\theta=\pm k\lambda \qquad (k=1,2,3,...,k \ne 0)
明纹条件:
asin\theta=\pm (2k+1)\frac\lambda{2} \qquad (k=1,2,3,...,k \ne 0)
角宽度和线宽度
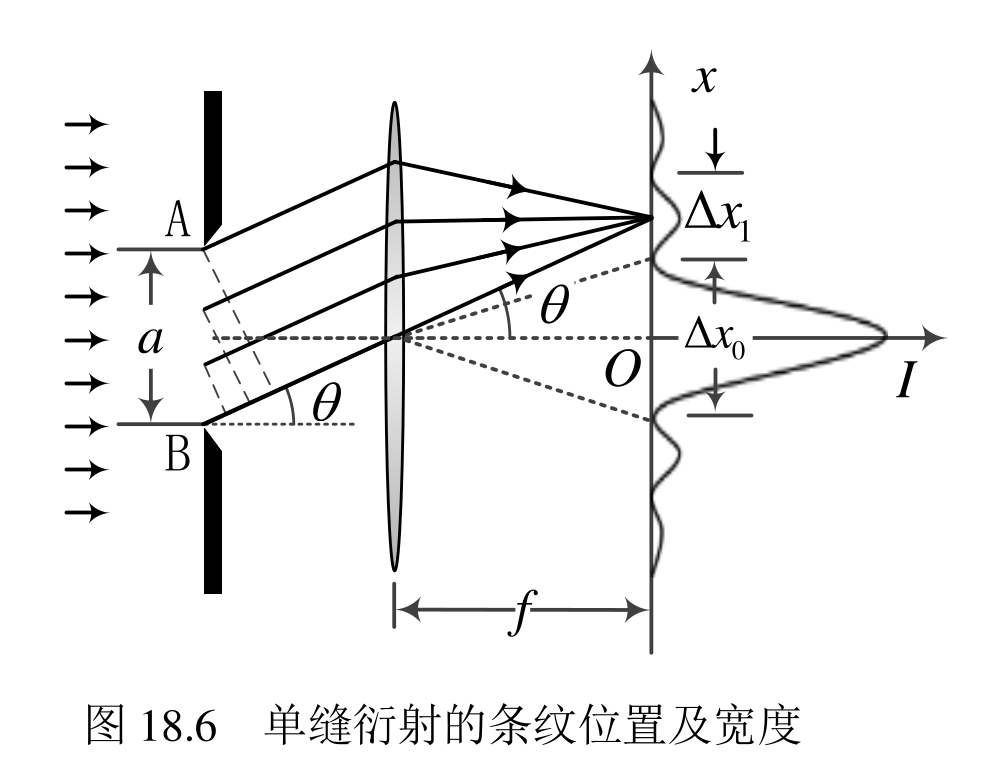
使用近似关系:
sin \theta \approx tan \theta \approx \theta
各级暗条纹衍射角:
\theta_k = arcsin\frac{k\lambda}{a} \approx \frac{k\lambda}{a}
角宽度:
\Delta\theta = \frac{\lambda}{a}
运用几何光学知识:
x=ftan\theta\approx f\theta
中央明纹线宽度:
\Delta x_0 = x_1 - x_{-1} = 2f\frac\lambda a
其他各级明纹线宽度:
\Delta x_k = x_{k+1} - x_{k} = f\frac\lambda a
注意以上结论涉及近似,仅在 \theta 很小的时候才成立。
圆孔衍射
衍射装置与衍射图样——艾里斑
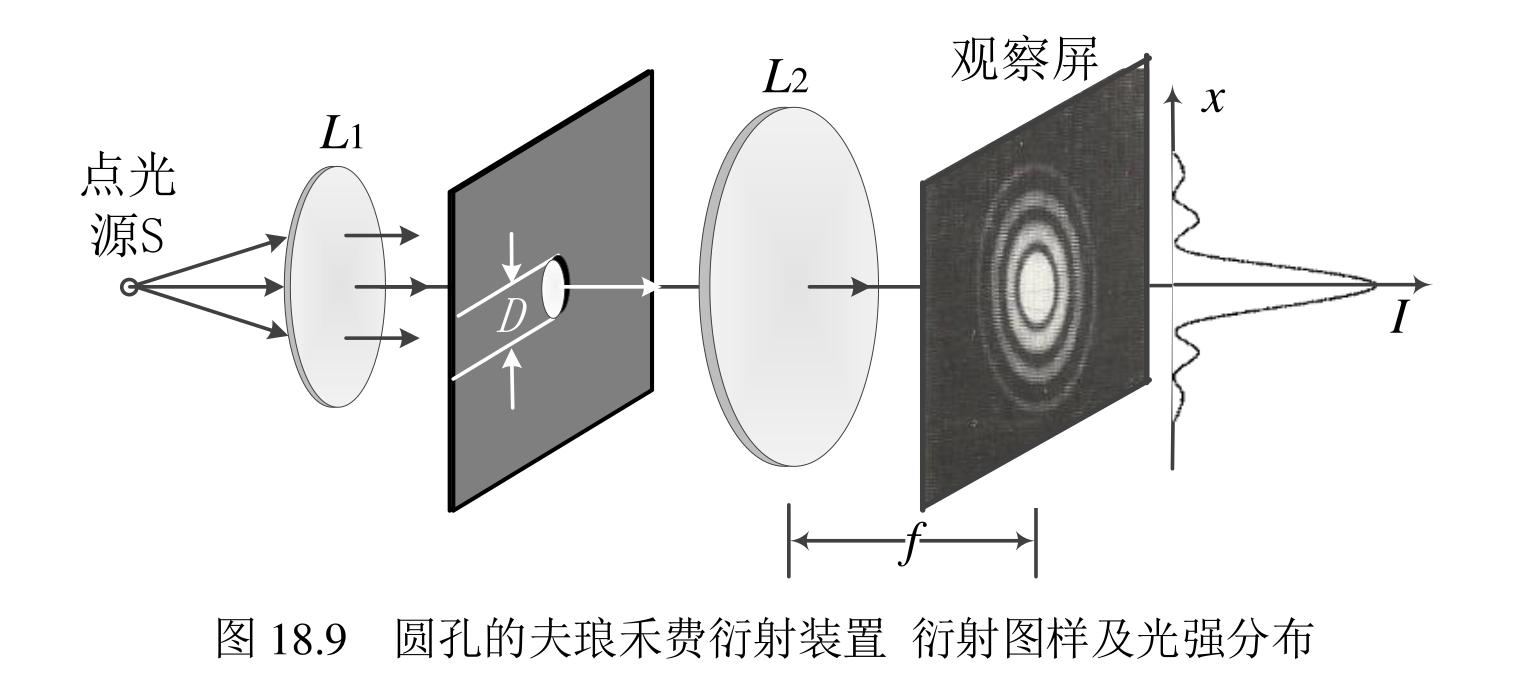
角半径公式(0.61是形状因子):
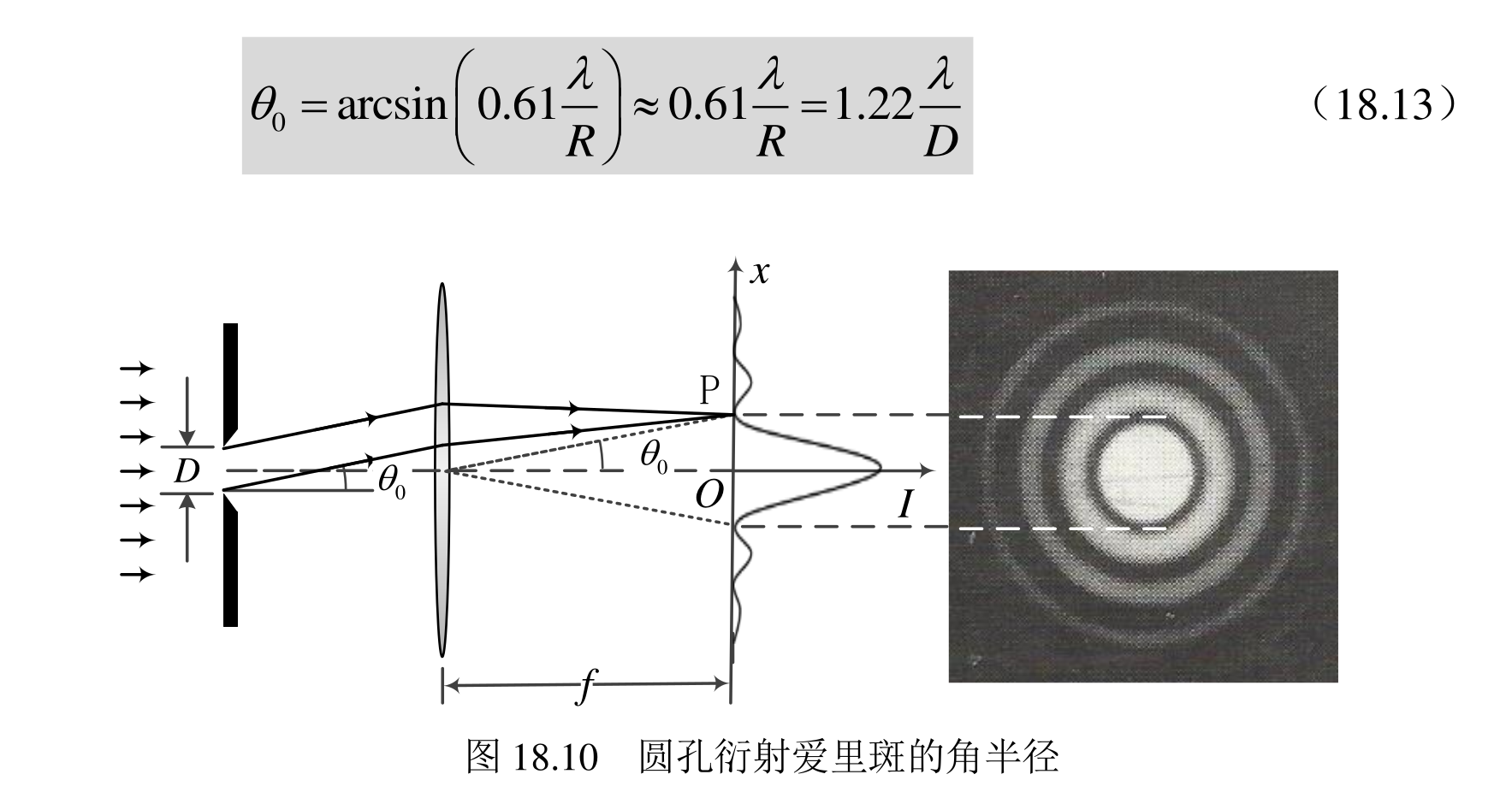
艾里斑半径:
r=ftan\theta_0 = 1.22\frac{\lambda f}D
光学成像仪器的最小分辨角和分辨本领
两个亮度相同的点物形成的艾里斑,当其中一个爱里斑的中心恰好位于另一个爱里斑的边缘时,这两个爱里斑恰好可以被分辨。
当两个点物所形成的像恰好能被分辨时,两个点物对透镜中心的夹角称为该光学仪器的最小分辨角,并用 \delta\varphi来表示。
即:
\delta\varphi = \theta_0 = 1.22\frac{\lambda}D
最小分辨角的倒数为光学仪器的分辨本领,用R(Resolution)表示:
R=\frac{1}{\delta\varphi}=\frac{D}{1.22\lambda}

