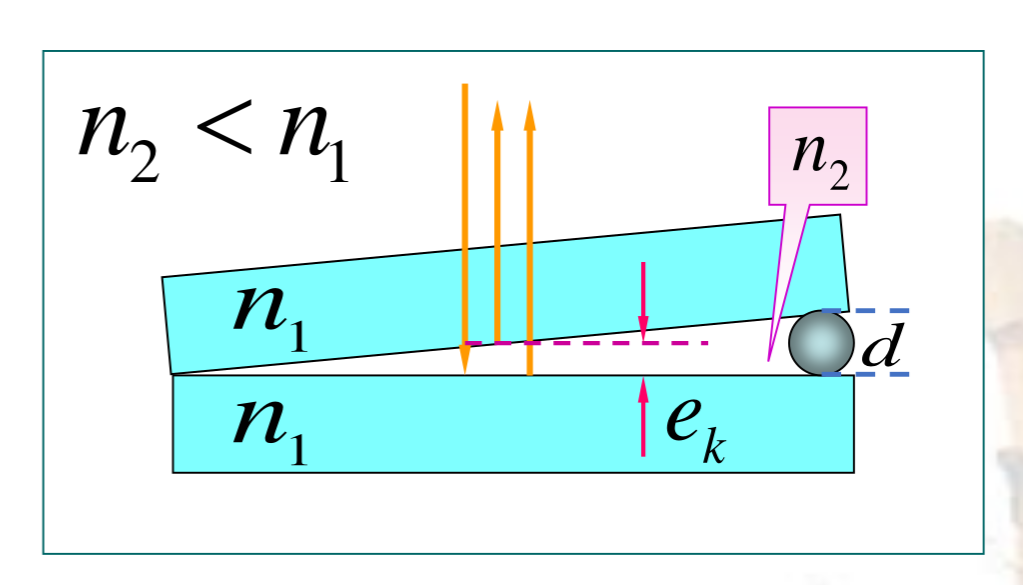
劈尖干涉
模型
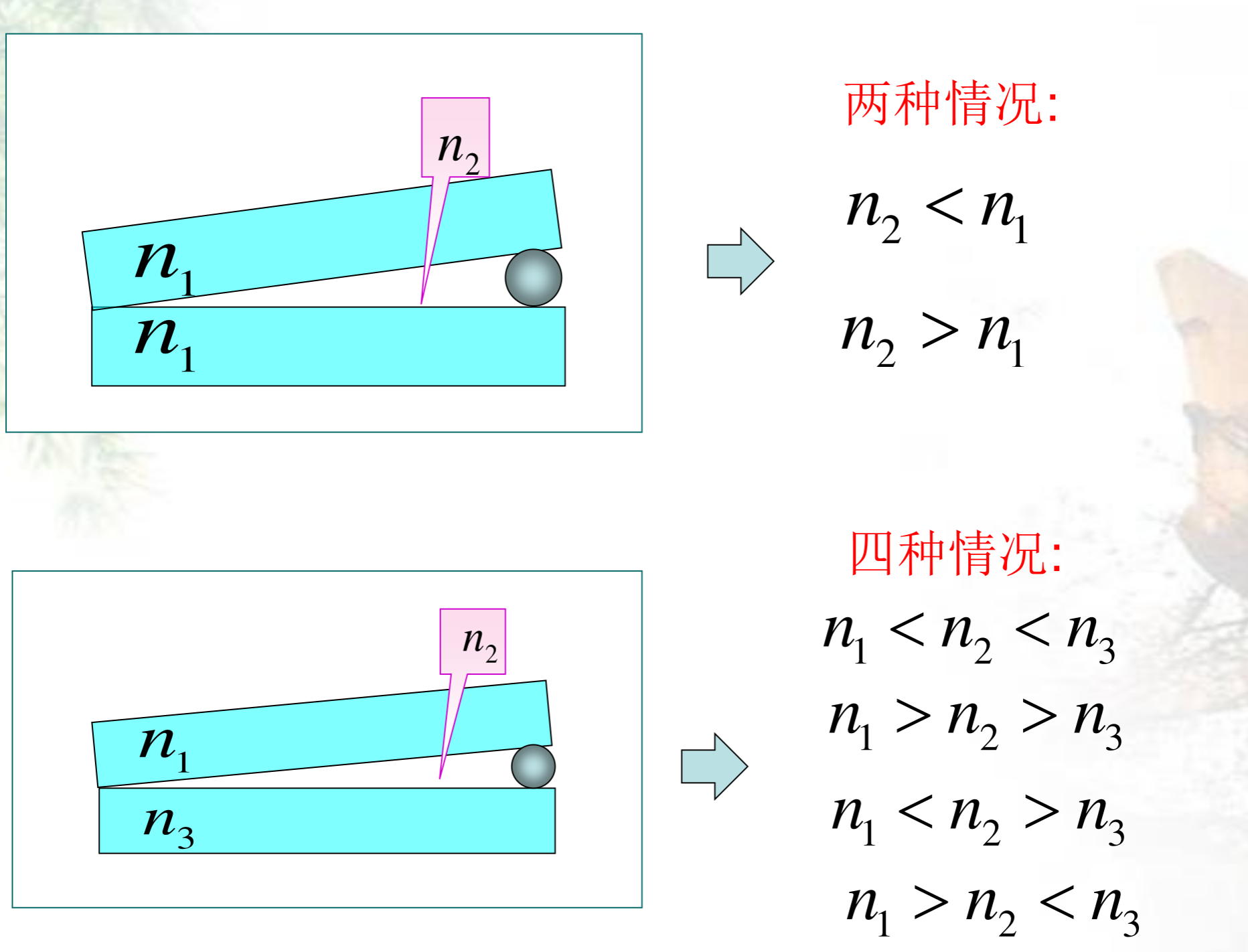
上下两板与中间的折射率均可以任取,于是便得到如下多种情况:
公式推理
劈尖干涉的间距公式(以标准模型为例):
\Delta = 2n_2e_k+\frac{\lambda}{2}
其中 \frac{\lambda}2为半波损失。
且根据干涉公式,具备:
\Delta=\left\{
\begin{aligned}
k\lambda & &,k=0,1,2 & &,明纹 \\
(2k+1)\frac{\lambda}2 & &,k=0,1,2 & &,暗纹 \\
\end{aligned}
\right.
联立解得:
e_k=\left\{
\begin{aligned}
(k-\frac{1}{2}\lambda)\frac{\lambda}{2n_2} & &,k=0,1,2 & &,明纹 \\
\frac{k\lambda}{2n_2} & &,k=0,1,2 & &,暗纹 \\
\end{aligned}
\right.
厚度差:
\Delta e=e_{k+1}-e_k = \frac{\lambda}{2n_2} = \frac{\lambda_2}2
水平间隔根据三角形相似求出:
\frac{d}{L} = \frac{\Delta e}{\Delta l}
显然,向上移动劈尖(加大劈尖间距)会使得水平间隔减小。
例题
例 1 波长为680 nm的平行光照射到L=12cm长的两块玻璃片上,两玻璃片的一边相互接触 ,另一边被厚度D=0.048 mm的纸片隔开.
试问在这12 cm长度内会呈现多少条暗条纹 ?
解
2e_k+\frac{\lambda}{2} = (2k+1)\frac{\lambda}2
解得
k=\frac{2d}{\lambda} = 141.1
此处即为临界点,故一共是142条(注意k=0)。
牛顿环
模型
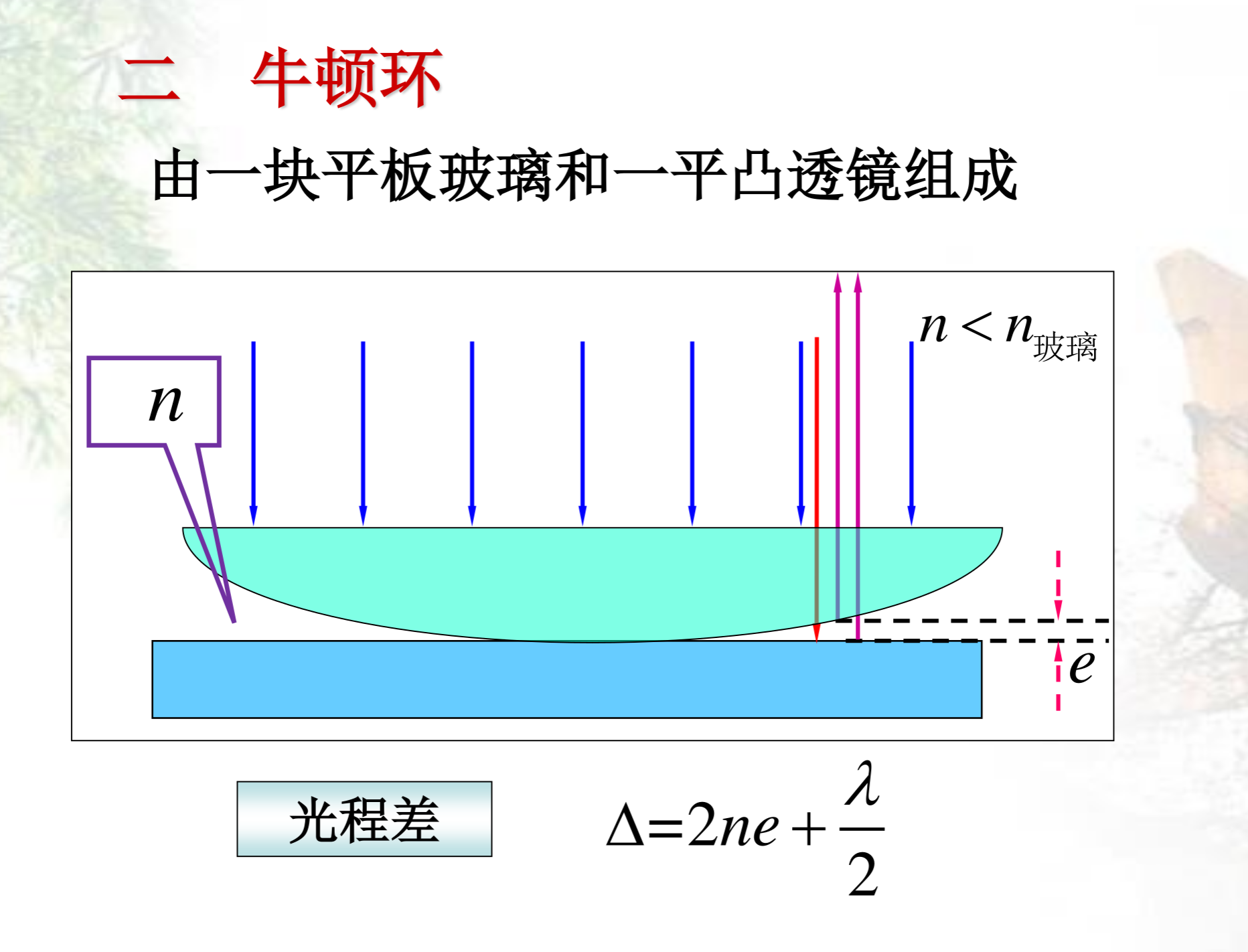
公式推理
与劈尖干涉类似,重点在于变成了圆弧。
仍具备如下公式:
e=\left\{
\begin{aligned}
(k-\frac{1}{2}\lambda)\frac{\lambda}{2n_2} & &,k=0,1,2 & &,明纹 \\
\frac{k\lambda}{2n_2} & &,k=0,1,2 & &,暗纹 \\
\end{aligned}
\right.
接下来进行几何推导:
\because R>>e \therefore e^2\approx0 \\
r^2 = R^2-(R-e)^2 = 2eR \\
r = \sqrt{2eR}
两式联立,解得:
r=\left\{
\begin{aligned}
\sqrt{\frac{2k-1}{2n}R\lambda} & &,明环 \\
\sqrt{\frac{k}{n}R\lambda} & &,暗环 \\
\end{aligned}
\right.
例题
例 2 如图所示为测量油膜折射率的实验装置,在平面玻璃片G上放一油滴,并展开成圆形油膜,在波长 600 nm 的单色光垂直入射下,从反射光中可观察到油膜所形成的干涉条纹.已知玻璃的折射率为 n1 = 1.50 ,油膜的折射率 n2 = 1.20 ,问:当油膜中心最高点与玻璃片的上表面相距 h = 8.0 *10 ^2 nm 时,干涉条纹是如何分布的?可看到几条明纹?明纹所在处的油膜厚度为多少?
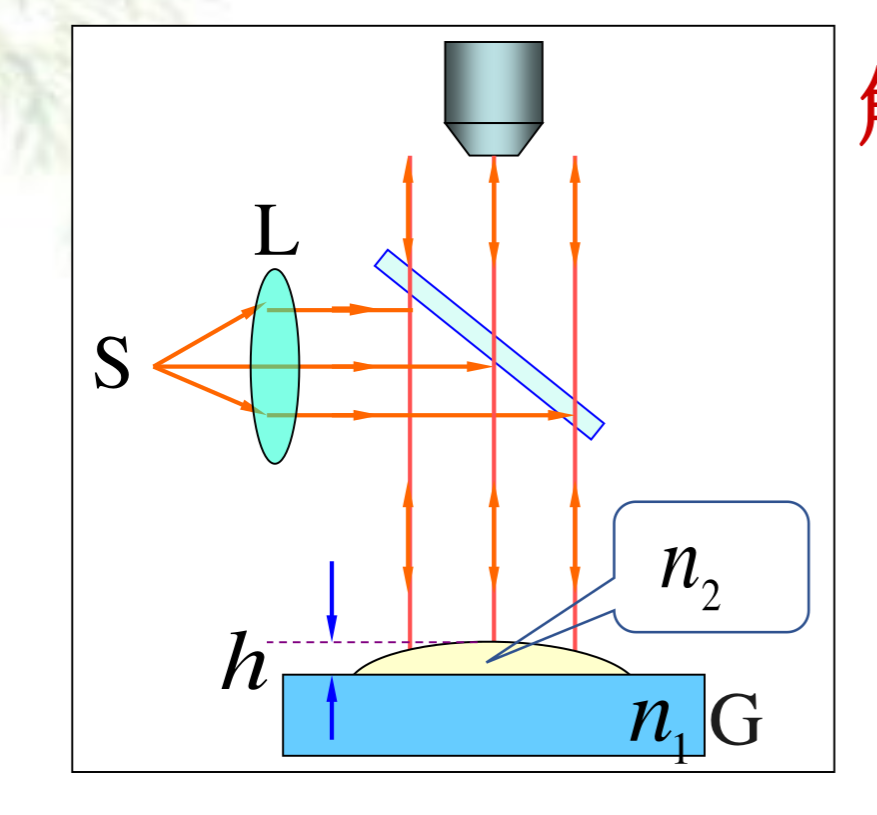
解 这个题目和传统的略有不同,不过仍然只需要按照相同方法进行正常推理即可。
根据公式(0级明条纹应该在最边上)
e=\frac{k\lambda}{2n_2}
可以得到
k=3,d=750nm \\
k=4,d=1000nm
因此k=3为临界点,共4条明纹。
例 3 用氦氖激光器发出的波长为633nm的单色光做牛顿环实验(中间空气),测得第 k 个暗环的半径为5.63mm , 第 k+5 暗环的半径为7.96mm,求平凸透镜的曲率半径R.
解 这个题目基本就是上个学期的实验题,直接代公式就行。
r_k=\sqrt{kR\lambda} \\
r_{k+5} = \sqrt{(k+5)R\lambda}
解得
R=\frac{r_{k+5}^2-r_k^2}{5\lambda}
迈克尔干涉
模型
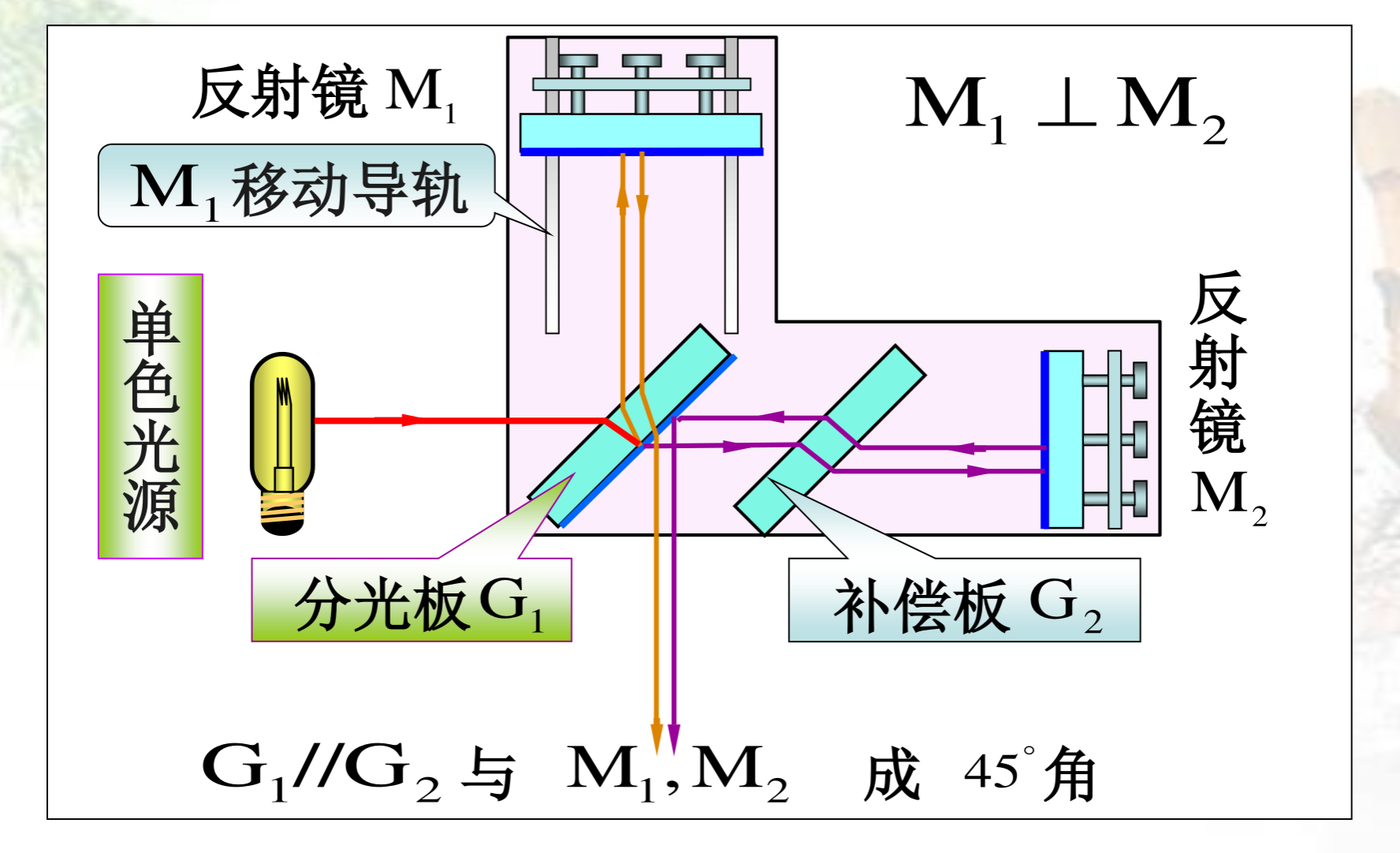
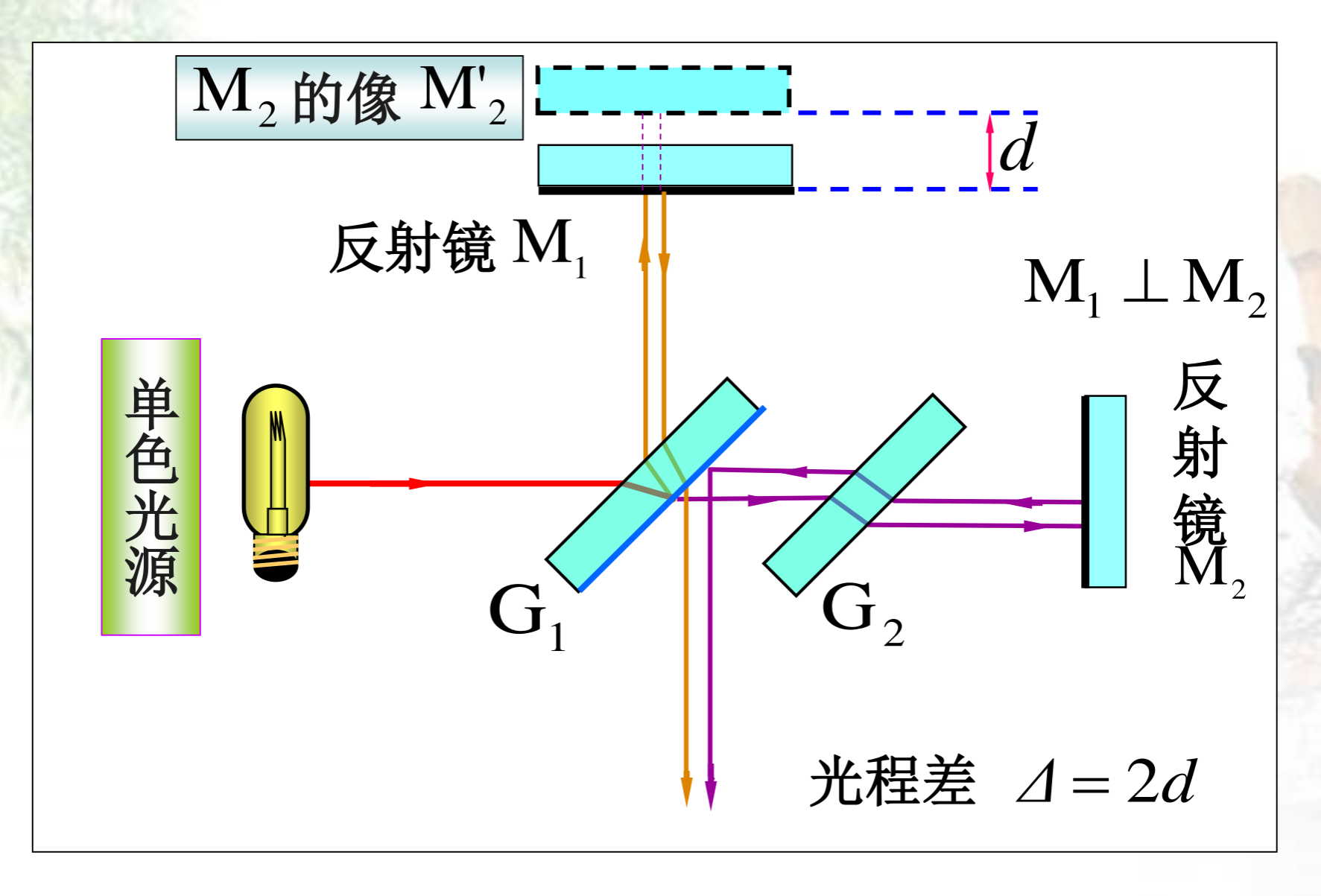
改变光程差的方式:
移动反射镜
在光路加入介质片
公式推导
中心处光程差:
\delta = 2e = \left\{
\begin{aligned}
k\lambda & &,k=0,1,2 & &,明纹 \\
(2k+1)\frac{\lambda}2 & &,k=0,1,2 & &,暗纹 \\
\end{aligned}
\right.
移动反射镜造成的光程差:
2\Delta e =\Delta k\lambda \\
\Delta e =\Delta k\frac{\lambda}2
插入介质片造成的光程差(t是厚度):
\Delta^{'}-\Delta = 2d - [2d+2(n-1)t] =2(n-1)t
其中-1是为了去除原本真空中已有的光程。
题目常涉及到干涉条纹的移动,于是有:
2(n-1)t = \Delta k \lambda
其中 \Delta k 是干涉条纹移动数目。
例题
例 4 在迈克耳孙干涉仪的两臂中,分别
插入 l = 10.0 cm长的玻璃管,其中一个抽成真空, 另一个则储有压强为 1.013 *10 ^ 5 Pa的空气 , 用以测量空气的折射率 n . 设所用光波波长为546 nm,实验时,向真空玻璃管中逐渐充入空气,直至压强达到1.013 *10 ^ 5 Pa为止 . 在此过程中 ,观察到107.2条干涉条纹的移动,试求空气的折射率 n
解 直接代公式就行:
2(n-1)t = 107.2\lambda\\
n=1.00029
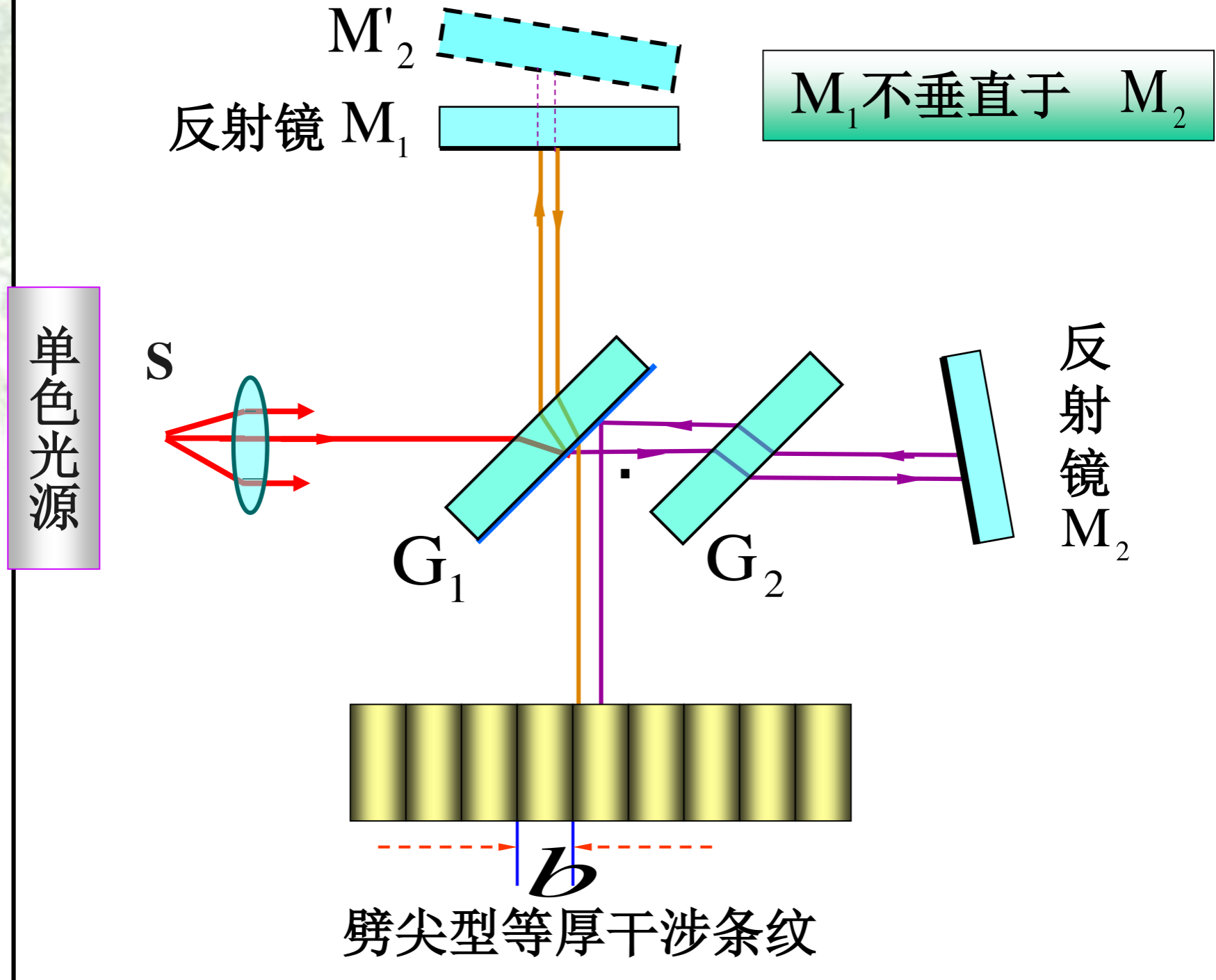
补充
当 M1不垂直于M2时,可形成劈尖型等厚干涉条纹。